樹齢の考察

ヤマザクラの樹齢

2018.3.17　鎌倉・峯山の会　藤井能成

1. はじめに

現在は、山頂の周辺のヤマザクラの群生する辺りの篠竹や真竹は2017年のほぼ1年間で刈り倒し、倒木や枯死して倒壊の恐れのある樹木は可能な範囲で伐採し、ヤマザクラに近づけるようになっている。Fig.1の写真は、現在（2018年1月）の峯山山頂付近の様子を示している。このような山頂の周囲に群生しているヤマザクラの巨木を見ているうちに、これらのヤマザクラはいつ頃植えられたものだろうかと興味を持つに至った。

常盤山緑地の西寄りに位置する峯山周辺にはヤマザクラの巨樹が群生している。昨年の冬から春にかけて、梶原口から桔梗山に通じる尾根道の両側にのびた笹などを切り開き、殿入り口から峯山に登るルートの倒木でふさがれた山道に巻き道を作ったりして散策路を切り開いていた。峯山の周囲は4~5mの高さの篠竹や真竹に覆われていて1~2m先も見通せない状態であったが、藪の上にはヤマザクラの花がかろうじて望めた。そこで峯山の頂に向かって人がやっと通れるほどの幅で篠竹を伐採し、辺りを覗いてみると倒木やアオキに覆われていた篠竹の藪の中にヤマザクラの驚くほどの巨樹が多数あり、そして倒木の7~8割がヤマザクラであることが分かった。しかしこのまま放置しておけば倒木が語るようにヤマザクラの巨樹もいずれ近いうちに枯れ果ててしまうだろうと思われた。

そこで、ヤマザクラの樹齢を推定する文献・資料を調査して見た。樹齢と胸高幹周り（ないし胸高直径）との関係を報告している資料としては、国土技術政策総合研究所の松江正彦室長らの「公園樹木管理の高度化に関する研究」という報告1）と、山本聡・高橋理喜男による「里山におけるヤマザクラ群生地の成立過程について」という報告2）が見いだされた。前者には元データは記載されていないが、樹齢に対する胸高幹周りの散布図と回帰式が記されている。後者には大阪近辺の二次林に生育しているヤマザクラについて調査した結果が報告されていて、樹齢と胸高直径のデータが示されている。樹齢は生長錐で採取した年輪サンプルの幅から推定したものである。このほかに、樹齢と胸高幹周りまたは胸高直径のデータが示されているものとして、渡辺典博、巨樹巨木（山と渓谷社、1999）3）がある。また、地方自治体のホームページ等にもそれぞれの地方のヤマザクラの名木の紹介があり、樹齢と幹周りのデータが示されている。

このほか、奈良県の吉野山のヤマザクラについて大規模な調査をした京都大学の吉野山サクラ調査チームの報告があるが、残念なことに樹齢と幹周りないし胸高直径との関係を示すデータは示されていなかった。樹齢と胸高直径との間には、狭い樹齢の範囲であれば回帰直線で表すことができると考えられる。樹木（の太さ）の成長には限りがあると考えられるので、樹齢の範囲を広くとった場合には直線関係が成り立たなくなると思われる。その場合には2次曲線の回帰式で表すこともできるが、樹齢tと胸高直径dとの関係に関してBertalanffyの1次の成長曲線の式4）がよく使われている。

d=D(1-exp(-g*t))……（1）

dは胸高直径、Dは到達可能な最大の胸高直径、gは成長速度、tは時間（樹齢）を示す。そこで、先にあげたデータを使って、それぞれの関係式について検討した。

2. ヤマザクラの樹齢と胸高幹周りとの関係

2.1 松江らの報告

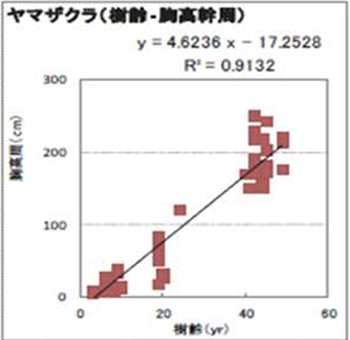
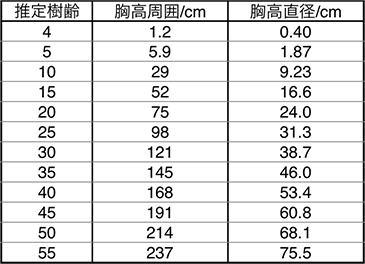
Fig.2は国土技術政策総合研究所の松江らの報告書に掲載されているデータのコピーである。元のデータの記載がないので、図中に示されている回帰式から調査範囲で胸高周囲を樹齢から逆算してTable.1に示した。
調査対象は公園や街路樹、苗木生産圃場などに植えられたヤマザクラであり、ヤマザクラにとっては好適な生育環境で良好に生育した樹木が選ばれていると記述されている。

2.2 山本・高橋氏らのデータ

大阪周辺の里山に生育しているヤマザクラの調査結果であり、松江らの調査対象より一般的なヤマザクラの生育環境で生育したヤマザクラが対象になっていると思われる。峯山も里山の環境にあるといえるのでより類似した環境の調査データであると考えられる。Table.2のデータをプロットするとFig.3のようになる。松江らのデータも重ねてプロットした。松江らのデータは胸高幹周り（BHP）で示しているので、胸高直径（BHD）はBHP/3.14として換算した。

両者の傾向はかなり異なり、同じ樹齢でも松江らの調査対象のヤマザクラの胸高直径は約2倍太く、成長速度が里山のヤマザクラより早いことを裏付けている。したがって、里山のヤマザクラの樹齢を推定するには、山本・高橋氏らのデータを使用する方がよいと考えられる。

回帰式は次式のようになる:t=2.0983*d-16.605…（2）

この式ではおよそ胸高直径で60~70cm程度、樹齢で130~140年程度までしか推定できない。さらに太い胸高直径のヤマザクラまでに補外できるかどうかは、ヤマザクラの成長にも限界があるはずであり樹齢とともに成長は遅くなると考えられるから、もっと高い樹齢のヤマザクラのデータを検討して見る必要がある。また、この回帰式には胸高直径が7.9cm以下の場合には樹齢が負になるとういう問題があり、胸高直径が8cm以上の場合にしか適用でしない。樹齢130年のデータが回帰直線より上の方にプロットされていることと、胸高直径には限界があること等を考え合わせると、直線で表現できる範囲は限られていて、樹齢と胸高直径との関係は下に凸の曲線になると考えられる。

なお、一般に最小二乗法で回帰式を当てはめる場合、当てはめた関数のX軸の変数（独立変数）で微分して正規方程式を得るため、Y軸の変数（従属変数）だけに誤差があるという前提に立つ。X軸の変数とY軸の変数両者に誤差がある場合には、例えばデミングの方法のような数値計算で回帰式に当てはめる方法5）がとられ、かなり複雑な計算になる。エクセルで回帰式を当てはめるデータ処理の方法ではそのような複雑な方法は採用していないと思われる。胸高幹周りは容易に実測できるが、樹齢は実測が困難であり、生長錐でサンプリングしても外側の一部のサンプルの年輪幅の平均値から樹齢を推定するので、精度は相対的に胸高幹周りあるいはそれから計算される胸高直径に比べてかなり劣ると考えられる。それ故ここでは、より誤差の小さいと考えられる胸高直径を独立変数（横軸）にとった。

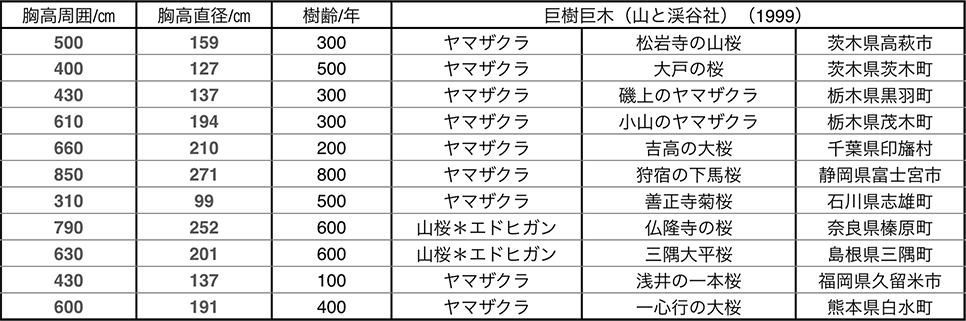
2.3 山と渓谷社「巨樹巨木」から抽出したヤマザクラのデータ

同書にはサクラ類の名木が非常に多数紹介されている。ヤマザクラやエドヒガンに加えて、カスミザクラ、サトザクラ、オオシマザクラ、紅枝垂れ、シダレザクラなどの種名で記述されていて分類がややこしい。ここでは、明らかにヤマザクラと示されているデータと2例のヤマザクラとエドヒガンザクラとの交配種のデータも加えて検討した。また、「巨樹巨木」の樹齢のデータは100年単位で示されており精度が悪い。統計処理で恣意的にデータを取捨選択することは避けなければならないが、回帰式の決定に使用できそうもない不正確と考えられる数値も含まれているので注意が必要である。

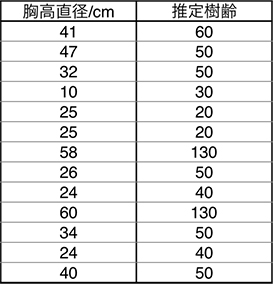
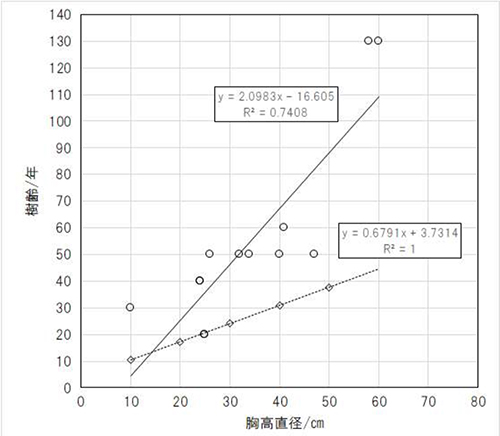
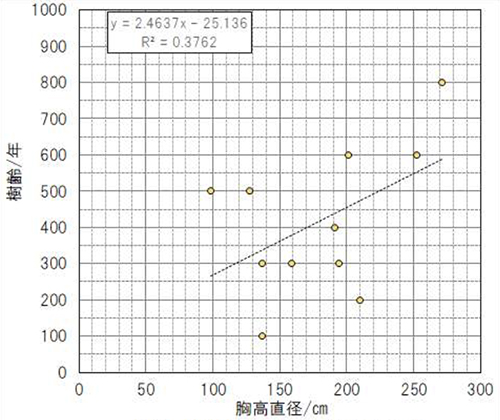
「巨樹巨木」から抽出したデータをTable.3に示し、Fig.4にプロットして示した。

図中に示す回帰式で計算される値と対応するデータとの相関係数は0.61で、回帰式による推定樹齢の傾向を37%程度しか説明できない。中には精度の良いデータもあるかもしれないが、伝聞や歴史資料から推定した樹齢データと推測される。そのためか100年単位で示されており、かなり荒っぽいデータである。それでも、‘大戸の桜’（BHD=127cm、樹齢=500年）、‘吉高の桜’（同210、200）、‘善正寺’の桜（同99、500）および‘浅井の一本桜’（同137、100）を除くとプロットは比較的狭い範囲に収まっている。

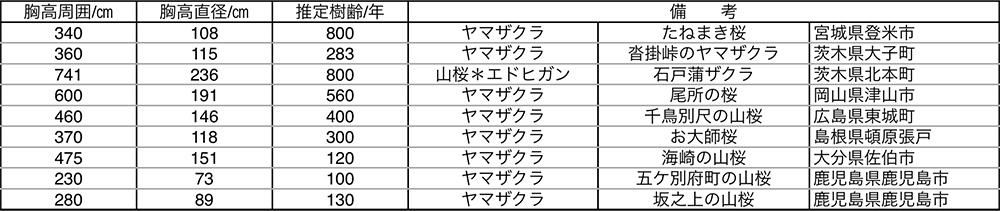
2.4 ホームページ等のデータ

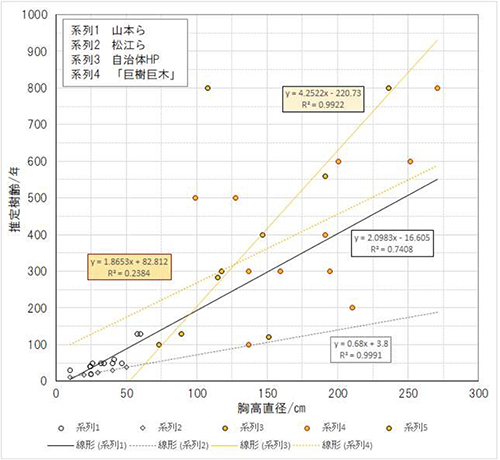
自治体等のホームページに紹介されているヤマザクラのデータをTable.4に、その散布図をFig.5に示した。Fig.5には松江らのデータと山本らのデータも重ねて示してある。

Table.4とFig.5のデータを見ると、胸高直径108cm、樹齢800年の登米市の‘たねまき桜’の点は、他のデータと比べて著しく胸高直径が小さい方に偏っている。また、胸高直径151cm、樹齢120年の佐伯市の‘海崎の山桜’は紹介記事の説明から生育環境が良好であるためか、松江らのデータの回帰直線の延長線のすぐ上にプロットされている。‘たねまき桜’と‘海崎の山桜’の2点を除くと、自治体等のホームページに記載されているデータは、おおむね山本らの調査データの回帰式の傾向に近いデータであると言えそうである。回帰直線の勾配が最も大きいのはホームページのデータによる回帰式で、山本らのデータに基づく回帰式の勾配はそれよりも小さく、松江らのデータからの回帰直線の勾配が最も小さい。なお、ホームページのデータの回帰直線では2つの特異的なデータを除いている。「巨樹巨木」のデータは広い範囲にばらついていて傾向をつかみ難い。回帰式で計算された樹齢と元のデータとの相関は2点を除いたホームページのデータが最も高く0.99で、山本らのデータで0.86、その寄与率は74%である。「巨樹巨木」のデータでは、相関係数は0.38とかなり低い。

これらのデータを比較すると、山本らのデータは胸高直径が60cm以下の樹齢の低い若い樹に当てはまり、ホームページのデータは胸高直径が70~200cm程度の比較的樹齢の高い樹に対応していると言えよう。

2.5 ヤマザクラの樹齢を推定する回帰式

［1］直線回帰式

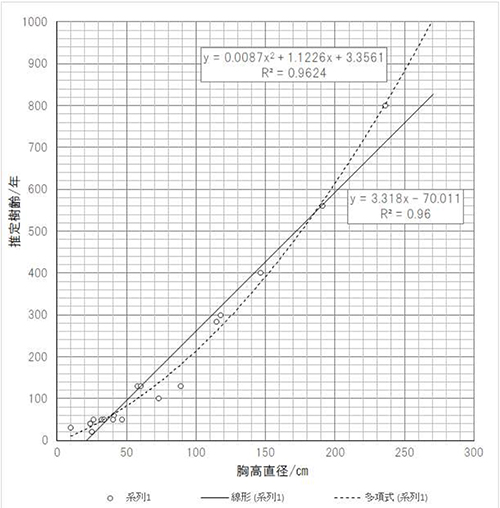
Fig.6に山本らのデータと自治体ホームページのデータから問題の2点を除いてプロットし、対応する直線帰式と2次曲線の回帰式を示した。

直線回帰式の場合には式で計算される樹齢とデータの樹齢との相関係数は0,97、寄与率は94%であり、2次曲線の回帰では相関係数は0.98、寄与率は96%で大差なく、十分に高い相関を示している。すなわちいずれの回帰式を使ってもある程度信頼できる樹齢が推定できると考えられる。しかし、詳しく見ると直線回帰式の場合、胸高直径30~200cm位の範囲では2点を除いてデータとよい近似をしているが、30cm以下200cm以上では樹齢を低く見積もる傾向がある。

2次曲線の回帰式の場合には樹齢の低い場合と高い場合にはよい近似をしているが、胸高直径50cm位から180cmの間では直線回帰式より樹齢を低く見積もる傾向がある。両者を比較すると、樹齢40~600年位まで、胸高直径で言えば30~200cmまでは、1次式の方が計算も簡単なので、樹齢推定には直線回帰式が簡便であろう。

t=3.318×d-70.011……（3）

2次式の回帰曲線も以下に示す。

t=0.0087×d^2+1.1226×d+3.3561……（4）

［2］Bertalanffyの成長曲線の式の当てはめ

先述の（1）式を変形して、次式に当てはめる。

t=(-1/g)×ln(1-d/D)……（5）

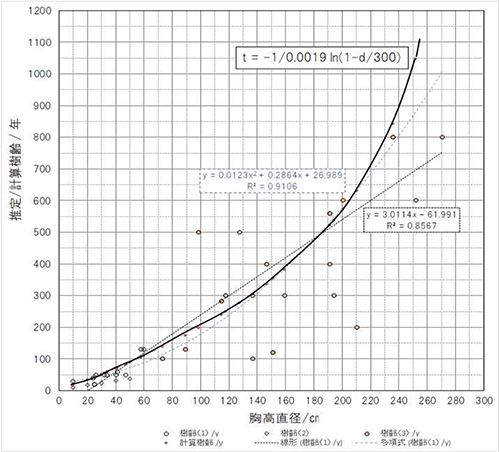
結果をFig.7に示した。直線回帰式と2次曲線の回帰式も比較して示した。山本らのデータと自治体ホームページから特異的な2点を除いたデータを使って、偏差平方和が最小になる成長速度gと最大胸高直径Dを求めると、次式のようになる。

t=(-1/0.0019)×ln(1-d/300)……（6）

この当てはめでは、山本らのデータに対しては相関係数が0.87、自治体ホームページのデータに対しては0.99、当てはめに使用したデータに対しては0.99と高い相関係数を示している。直線回帰式と比べると、胸高直径60~190cmの範囲では樹齢を低く見積もり、60cm以下および190cm以上では高く見積もることになる。2次曲線の回帰式とは胸高直径60~130cmの範囲と210cm以上では2次の回帰直線の方が低く推定される。しかし、樹齢の広い範囲で適用できると考えられるので、ヤマザクラの樹齢の推定にはこの（6）式が適当と考えられる。関数電卓やPCが使える環境であれば（6）式を使うことは難しくないだろう。

3. 峯山のヤマザクラの樹齢

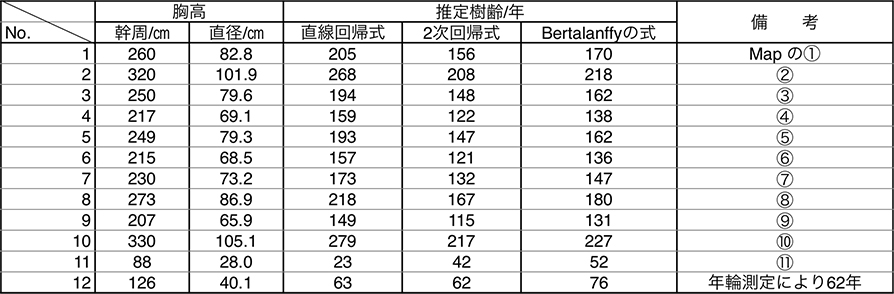
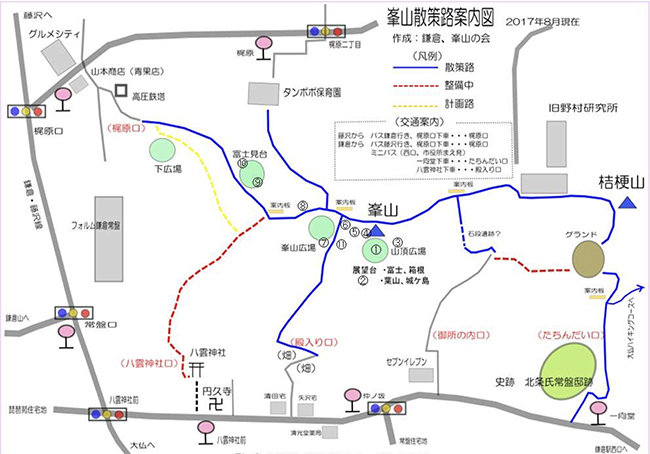
峯山の周辺には驚くほど多数のヤマザクラが群生しているが、そのうちから代表的な樹を選んで胸高幹周りを計測した。胸高幹周りの値とそれから求めた胸高直径、直線回帰式（3）と2次回帰式（5）、およびBertalanffyの回帰式（6）で推定した樹齢をTable.5に示した。それらの生えている場所をFig.8に示す。

これらの値を比較すると、胸高直径が40cm以下では直線回帰式による計算値は2次回帰式およびBertalanffyの式で得られた樹齢より低くなり、40cmを超える胸高直径では直線回帰式で計算される樹齢の方が大きくなる。2次回帰式で計算される樹齢はBertalanffyの式で計算される樹齢より低い値が得られる。いずれが妥当な推定値かは100年以上の樹齢の信頼性の高いデータがもっと多く得られないと評価が難しい。しかしいずれにせよ、峯山に群生する大多数のヤマザクラの樹齢は100数十年から250年位と推定される。江戸時代後半から明治時代に植えられた樹であると思われ、後世に伝えられるべき文化的資産であると言えよう。

引用文献・資料
1）松江正彦ら:「公園樹木管理の高度化に関する研究」、国土技術政策総合研究所緑化生態研究室報告書（2010年度）.
2）山本聡・高橋理喜男:「里山におけるヤマザクラ群生地の成立過程について」、造園雑誌54（5）,p.173-178（1991）.
3）渡辺典博、巨樹巨木（山と渓谷社、1999）.
4）篠崎吉郎、化学と生物、Vol.17,No.3（1979）, 187-189.
5）W.E.デミング、推計学によるデータのまとめ方（岩波書店、1962）.

以上